| Titel: | Ueber die zweckmäßigsten Verbindungscurven für Eisenbahnen; von Prof. G. Decher. |
| Autor: | Georg Decher [GND] |
| Fundstelle: | Band 170, Jahrgang 1863, Nr. II., S. 4 |
| Download: | XML |
II.
Ueber die zweckmäßigsten Verbindungscurven für
Eisenbahnen; von Prof. G.
Decher.
Mit einer Abbildung auf Tab. I.
Decher, über die zweckmäßigsten Verbindungscurven für
Eisenbahnen.
Alle Erbauer von Eisenbahnen halten meines Wissens noch an dem Gebrauche fest, sich
kreuzende Bahnrichtungen durch Kreisbogen zu verbinden,
obgleich diese Verbindungsart wesentliche Nachtheile mit sich führt, sowohl in Bezug
auf die Annehmlichkeit und Sicherheit des Fahrens, als in Bezug auf die
Dauerhaftigkeit der Wagen und Schienen. Denn bei jeder Bewegung in vorgeschriebener
Bahn übt bekanntlich der sich bewegende Körper auf diese Bahn einen nach der
Verlängerung des Krümmungshalbmessers gerichteten Druck aus, welcher bei gleicher
Geschwindigkeit und Masse des Bewegten der Krümmung der
Bahn proportional ist; da nun der Kreis eine constante Krümmung besitzt, so
muß auch jener Druck bei constanter Geschwindigkeit des Bewegten von Anfang an bis
zum Ende der kreisförmigen Bewegung ein constanter seyn, er wird daher beim Eintritt
in den Kreisbogen plötzlich mit seiner ganzen Stärke auftreten und bei dem Austritt
aus demselben in eine geradlinige Bahn plötzlich verschwinden, und die Folgen dieses
plötzlich auftretenden und verschwindenden Bewegungsdruckes können für einen
Wagenzug nur sehr nachtheilig seyn.
Wenn sich ein Wagenzug in einem krummlinigen Geleise bewegt, so drückt jeder
Wagenkörper in Folge dieser Bewegung in der Art auf die Radachsen, daß er diese nach
ihrer Länge zu verschieben strebt; dadurch werden dann auch die äußeren Räder mit
ihren Spurkränzen seitwärts gegen das äußere Geleise gedrückt und steigen wegen der
concaven Form des Spurkranzes an diesem Geleise etwas an. Dieses Ansteigen wird dann
durch die wälzende Bewegung der Räder unter Mitwirkung der aus jenem Druck folgenden
Seiten-Reibung zwischen Spurkranz und Geleise wesentlich vermehrt, und es
kann schon dadurch bei starker Krümmung der Bahn, großer Geschwindigkeit des Zuges
und rauher Oberfläche der Schienen dahin kommen, daß sich die äußeren Räder auf die
Schienen hinaufwälzen und die Wagen entgleisen. Tritt nun aber ein Wagenzug mit
constanter Geschwindigkeit aus einem geradlinigen Geleise in ein kreisförmiges ein,
so erfolgt die erwähnte kleine Verschiebung der Wagen nach Außen plötzlich mit dem
Eintritt in den Kreisbogen unter einem fühlbaren Ruck, und zu jenem Bewegungsdruck,
der von der Geschwindigkeit der Bewegung und von der Krümmung der Bahn abhängt,
kommt in Folge des mit jener plötzlichen Verschiebung verbundenen Stoßes noch ein
neuer Druck, der zwar nur kurze Zeit wirkt, aber durch seine Größe die Gefahr des
Entgleisens unter sonst gleichen Umständen zu einer viel bedenklicheren Höhe
steigern kann. Fährt dann der Zug wieder aus dem kreisförmigen Geleise in ein
geradliniges ein, so hört der Bewegungsdruck plötzlich auf, und die Wagen stellen
sich mit einem neuen Ruck seitwärts gleitend wieder in das horizontale
Gleichgewicht, so daß also bei jedem Ein- und Austritt eines Wagenzuges aus
einem geradlinigen Geleise in ein kreisförmiges und umgekehrt, ein stoßweises
Hinüber- und Herüberrutschen der Räder auf den Schienen und der Wagenkörper
auf den Achsen der Räder, soweit es der nothwendige Spielraum der Achsenlager
zuläßt, stattfindet, was abgesehen von der Gefahr des Entgleisens weder die Annehmlichkeit des Fahrens
zu erhöhen, noch die Dauerhaftigkeit der Schienen, Räder und Achsen zu vermehren
geeignet ist.
Soll die Gefahr des Entgleisens dadurch vermindert werden, daß wie es jetzt
gewöhnlich geschieht die äußeren Schienen im kreisförmigen Geleise erhöht werden, so
werden die eben besprochenen Nachtheile um nichts vermindert; denn beginnt die
Erhöhung erst mit dem Anfang der Curve, so sind hier alle Verhältnisse dieselben wie
vorher; dann erfüllt aber auch diese Erhöhung ihren Zweck nicht, weil, wie gezeigt
wurde, die Gefahr des Entgleisens gerade am Anfang des Kreisbogens die größte ist
und weil deßhalb die Erhöhung der äußeren Schiene, wenn jener Zweck erfüllt werden
soll, hier schon wenigstens ebenso groß seyn muß, als sie überhaupt für diesen
Kreisbogen nothwendig ist. Es muß daher zweckentsprechend jene Erhöhung der äußeren
Schiene noch in der geradlinigen Strecke beginnen und endigen, da sie nur eine
allmähliche seyn kann, und es wird damit das Hinüber- und Herüberrutschen der
Wagen offenbar vermehrt, der Stoß beim Ein- und Austritt in und aus dem
Kreisbogen aber keineswegs beseitigt.
Noch größer aber sind diese Uebelstände bei dem Uebergange von einem Kreisbogen zu
einem anderen mit entgegengesetzt gerichteter Krümmung, welcher auch ziemlich oft
vorkommt, da hier der Bewegungsdruck plötzlich so zu sagen in die entgegengesetzte
Richtung umspringt und die Wagen daher mit einem viel stärkeren Stoß auf die andere
Seite geworfen werden, und weil hier die Gefahr des Entgleisens, welche wegen dieses
Stoßes gerade bei dem Wechsel der Krümmungsrichtung unter sonst gleichen
Verhältnissen die größte ist, nicht durch einseitige Erhöhung der Schienen
vermindert werden kann.
Allen diesen Uebelständen weicht man aus, wenn statt der Kreisbogen solche Curven zur
Verbindung sich kreuzender Bahnrichtungen angewendet werden, deren Krümmung mit Null anfängt, bis zur Mitte der Curven allmählich wächst und
dann wieder bis Null abnimmt. Denn in einer solchen Curve wird auch der
Bewegungsdruck von Null an allmählich bis zur Mitte derselben wachsen und dann
wieder bis Null abnehmen; beim Uebergang von einer Curve in eine entgegengesetzt
gekrümmte wird er nicht plötzlich die Richtung wechseln, sondern immer erst Null
werden und dann erst wieder im entgegengesetzten Sinne wachsen; damit muß dann auch
das Verschieben der Wagenkörper auf den Radachsen und der Räder auf den Schienen in
einer stetigen Bewegung stattfinden; endlich wird durch das Wegfallen des plötzlich
auftretenden dynamischen Druckes und des damit verbundenen Stoßes auf die äußere
Schiene beim Eintritt in die Curve die Gefahr des Entgleisens so sehr vermindert, daß auch ohne
einseitige Erhöhung des Geleises nur bei sehr extremen Verhältnissen wirkliche
Gefahr zu befürchten ist; will man aber, um nichts zu versäumen, die äußeren
Schienen erhöhen, so darf auch diese Erhöhung nur mit dem Anfang der Curve beginnen,
allmählich bis zur Mitte derselben wachsen und sich bis zum Ende wieder ganz
verlieren, und es macht dabei keinen Unterschied, ob die Curve sich an ein
geradliniges Geleise anschließt, oder an eine andere Curve von gleich- oder
von entgegengesetzt-gerichteter Krümmung.
Curven von der bezeichneten Art gibt es eine unbegrenzte Menge; sie kennzeichnen sich
in der Gestalt augenfällig dadurch, daß sie in zwei Punkten eine Wendung machen oder
die Krümmungsrichtung wechseln und daher in diesen Punkten, welche für unsern Zweck
den Anfang und das Ende der Verbindungscurve bilden, von der Tangente geschnitten
werden. Es ist jedoch nicht einmal nothwendig, daß die Verbindung aus einer einzigen
Curve besteht, sie kann auch aus zwei congruenten und selbst, wenn besondere
Umstände es nothwendig machen, aus zwei nicht congruenten Curvenstücken bestehen,
welche in ihrem Vereinigungspunkt den Krümmungskreis gemeinschaftlich haben, und es
genügt deßhalb unserem Zwecke eine Curve, welche nur einen Wendepunkt besitzt. Aber auch diese augenfällige Eigenschaft der
Wendung ist für unsere Verbindungscurve nicht absolut nothwendig; denn es gibt auch
eine unbegrenzte Menge Curven, welche die für unsern Zweck allein nothwendige
Eigenschaft, daß wenigstens in einem ihrer Punkte die Krümmung
Null ist, besitzen, ohne daß die Krümmung in diesem Punkte die Richtung
ändert und die Curve dort von der Tangente geschnitten wird. Diese allein
nothwendige Eigenschaft wird am einfachsten durch die analytische Bedingung erkannt
und erhalten, daß für den betreffenden Punkt die zweite Ableitung der Function,
welche die eine der rechtwinkeligen Coordinaten durch die andere ausdrückt, Null
werden muß, daß also, wenn
y = f(x)
die Gleichung der betreffenden Curve in Bezug auf beliebige
rechtwinkelige Coordinatenachsen ist, für den Punkt, welcher den Anfang der
Verbindungscurve bilden soll,
d²y
=f''(x) = 0
dx²
werden muß.
Die Verschiedenheit der Gestalten aller dieser Curven gestattet dem Ingenieur auch,
den Terrain-Verhältnissen mehr oder leichter Rechnung zu tragen, als es bei
der Kreisbogen-Verbindung möglich ist, wenn sich derselbe nicht scheut, auch
Curven anzuwenden, deren Gleichungen nicht die möglichst einfachen sind; denn der
Kreisbogen hat nur ein Bestimmungsstück, den Halbmesser, während sich leicht Curven
der oben bezeichneten Art mit mehreren und selbst beliebig vielen Bestimmungsstücken
finden lassen. Ich werde mich jedoch hier auf die Erörterung derjenigen Curven
beschränken, welche ich für die einfachsten und zweckentsprechendsten halte und für
welche ein einziges Bestimmungsstück genügt; der mathematisch gebildete Ingenieur
wird darnach vorkommenden Falles auch zusammengesetztere Gleichungen, von denen ich
einige andeuten werde, zu behandeln wissen.
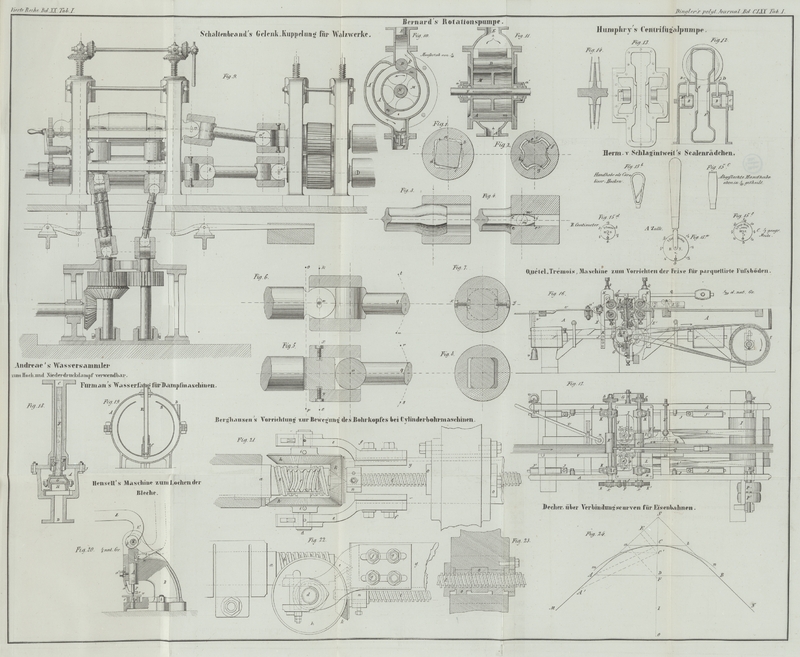
Wenn nun MS und SN, Fig.
24, die zu verbindenden Bahnrichtungen sind, so ist der von ihnen
eingeschlossene Winkel MSN = 2α immer als gegeben vorauszusetzen; außer diesem
muß aber wenigstens noch ein weiteres Bestimmungsstück gegeben seyn, damit die
Aufgabe eine bestimmte wird, wenn man über die Art der Verbindungscurve ACB eine Wahl getroffen hat. Die im Allgemeinen
wichtigsten dieser Bestimmungsstücke sind:
1) der Abstand SC = f
des Scheitels C der Curve von dem Schnittpunkt S der zu verbindenden Bahnrichtungen oder der Tangenten
AS und BS im
Anfangs- und Endpunkt der Verbindungscurve, die hier immer symmetrisch zu
beiden Seiten des Scheitels C vorausgesetzt wird, so daß
die SC den Winkel MSN halbirt,
2) die Länge AS = BS = t der genannten Tangenten,
3) der Krümmungshalbmesser CO = ρ im Scheitel der Curve, also der kleinste
Krümmungshalbmesser derselben.
Es wird sich dann darum handeln, die Beziehungen aufzusuchen, welche zwischen diesen
Stücken und der einzigen nothwendigen Constanten der gewählten Curvengleichung
bestehen, um diese Constante nach einem jener Bestimmungsstücke und umgekehrt diese
aus der Constanten berechnen zu können. Für die Wahl der Curvengleichung endlich,
fofern es sich um möglichst einfache Gleichungen handelt, wird zunächst maßgebend
seyn, ob die Curve von den Tangenten AS und BS oder von der Sehne AB aus abgesteckt werden soll, d.h. ob man jene Tangenten oder diese Sehne
als Abscissen-Achsen nehmen und die dazu senkrechten Ordinaten der
Curvenpunkte nach gegebenen Abscissen berechnen und abmessen will; denn es wird
einleuchten, daß ein und dieselbe Curve nicht sowohl auf die Sehne wie auf die
Tangente bezogen durch eine gleich einfache Gleichung ausgedrückt seyn kann, und daß
es deßhalb nothwendig seyn wird, für jede der genannten Abscissenachsen andere
Curven zu wählen. In den meisten Fällen dürfte das Abstecken von den Tangenten aus
das zweckmäßigste seyn,
weil diese Geraden jedenfalls schon bestimmt, abgesteckt und zugänglich gemacht
sind, während die Sehne erst noch abgesteckt werden muß und auch meistens,
namentlich bei der Umgehung von vorspringenden Hügel- oder Bergrücken und von
Flußkrümmungen viel weniger zugänglich ist, als die Tangenten, dann aber auch weil
die Ordinaten von der Sehne aus immer größer sind, als von der Tangente aus, und
daher das Abstecken von den letzteren weniger Zeit erfordert, und bei gleicher
relativer Genauigkeit der Messung eine größere absolute Genauigkeit gewährt, als das
von der Sehne aus; ich will jedoch im Folgenden für beide Arten des Absteckens die
einfachsten Curven erörtern.
I. Curven von der Sehne aus.
Beim Abstecken von der Sehne aus kann man entweder die Mitte D oder einen der Berührungspunkte A oder B als Anfang der Abscissen nehmen. Im ersten Falle ist
es natürlich eine einzige zu beiden Seiten von CD
symmetrische Curve zur Verbindung zu wählen. Die Gleichung einer solchen Curve hat
dann die Bedingungen zu erfüllen, 1) daß die y für
positive und negative x gleich bleiben, 2) daß y und d²y/dx² für die Punkte
A und B Null wird, 3)
daß dy/dx für
diese Punkte = ± cotang α, für C aber Null wird. Die beiden einfachsten Gleichungen für
Curven dieser Art sind daher
y = a +
bx² + cx⁴
und y = b cos x/a.
Ich bringe die erste unter die homogene Form:
y = h (1 + α
x²/a² + β
x⁴/a⁴)
und ziehe daraus
dy/dx = 2h/a
(α x/a + 2β x³/a³), d²y/dx² = 2h/a² (α + 6β
x²/a²).
Es ist dann in C für x = 0,
y = h = CD, dy/dx = 0, und wenn a =
AD = BD die
halbe Sehne bedeutet, so folgen nach den obigen Bedingungen für die Punkte A und B oder für x = ± a die
Gleichungen:
0 = 1 + α + β, 0 = α + 6β, 2h/a (α + 2β) = – cot
α
und damit ergibt sich
α = – 6β, β = 1/5 = a/8h cot α, h = 5/8 a cot α.
Unsere Curvengleichung nimmt damit die bestimmte Form an:
1) y = 1/8a cot α (5
– 6 x²/a² + x⁴/a⁴),
worin nun a die einzige
nothwendige Constante ist, und man findet leicht für unsere Bestimmungsstücke die
Beziehungen:
t = a/sin
α, f = a cot α – h = 3/8 a cot
α = 3/8 t cos α
Textabbildung Bd. 170, S. 10
durch welche jedes derselben aus jener Constanten a oder diese aus einem von ihnen berechnet werden
kann.
Die zweite der obigen Curven-Gleichungen wird am besten auf die Form:
y = h cos π/2 x/a
gebracht, worin h und a dieselbe Bedeutung haben wie vorher; denn man hat für
x = 0, y = h und für x = ± a, y = 0.
Ferner wird
dy/dx = – π/2 h/a sin
π/2 x/a, d²y/dx² = –
π²/4 h/a² cos π/2 x/a,
und man zieht daraus
für x = 0, dy/dx = 0, d²y/dx² = – π²/4 h/a²,
für x = a
dy/dx = – cot α = – π/2 h/a,
d²y/dx² = 0;
die bestimmte Form unserer Gleichung ist demnach
2) y = 2/π a cot α cos
x/a 90°,
wobei die Sexagesimaltheilung zu Grunde gelegt ist, und für
unsere Bestimmungsstücke ergeben sich die Beziehungen:
t = a/sin α, f = a cot α – h = π – 2/π a cot α =
π – 2/π t cos
α,
ρ = 4/π²
a²/h = 2/π a tang α =
2/π t sin²α/cos α.
Die Vergleichung der aus den beiden Curvengleichungen (1) und (2) gezogenen Werthe
für f und ρ zeigt,
daß sich beide Curven in der Form nur wenig unterscheiden, und daß die algebraische
Gleichung (1) für dasselbe
a oder t nur etwas größere,
also günstigere Werthe für f und ρ gibt; wo dieß aber nicht von Belang ist, dürfte sich die
goniometrische Gleichung (2) der einfacheren Berechnung wegen mehr empfehlen.
Diese letztere bietet auch den Vortheil, daß sie leicht in eine eben so einfache für
den Punkt A als Anfang der x
zu verwandeln ist, sie wird nämlich dazu und zwar von A
bis B, wie man sich leicht überzeugen wird, und die +
x von A gegen B gerechnet,
3)
y = 2/π a cot α
sin π/2 x/a,
und es bleiben dabei alle Beziehungen zwischen a, t, f und ρ
unverändert.
Eine algebraische Gleichung für den Anfang A läßt sich
zwar auch leicht durch die Substitution a – x für x in Gleichung (1)
ableiten; da es aber, wie oben bemerkt, nicht nothwendig ist, daß die
Verbindungscurve ACB aus einer Curve besteht, daß also in der zu suchenden Gleichung auch für x = 2a die Werthe für y und d²y/dx² Null werden, da
es vielmehr genügt, daß die Verbindung aus zwei Curven AC und BC besteht, welche in C die Tangente und den Krümmungskreis gemeinschaftlich
haben, so kann man sich auf die einfachere Form:
y = k
(α x/a + β
x³/a³)
beschränken, und diese den Bedingungen unterwerfen:
x = 0, y
= 0, dy/dx = cot α,
d²y/dx² = 0,
x = a,
dy/dx = 0.
Man findet damit wie vorher die bestimmtere Form:
4)
y = 1/2h (3 x/a – x³/a³) = 1/3 a cot α (3 x/a –
x³/a³)
und die Beziehungen:
t = a/sin
α, f = a cot α – h =
1/3a cot α,
ρ = a²/3h = 1/2a tang α =
1/2t sin²α/cos α.
Diese Werthe für f und ρ sind übrigens noch weniger vortheilhaft, als die aus (2) oder (3)
hervorgehenden.
Soll die Gleichung der Verbindungscurve mehr als einem Bestimmungsstücke genügen und
demnach mehrere nothwendige Constanten enthalten, so darf man die algebraischen
Gleichungen nur um Glieder mit höheren Potenzen vermehren, so daß die Gleichung (1) in
die allgemeinere Form:
y = b₀ + b₂ x²/a² + b₄ x⁴/a⁴ + b₆ x⁶/a⁶ + etc.
die Gleichung (4) dagegen in
y = b₁ x/a + b₃ x³/a³ + b₅ x⁵/a⁵ + etc.
übergeht; die goniometrischen Gleichungen dagegen müssen um
ähnliche Glieder mit den ungeraden Vielfachen von π/2 x/a vermehrt werden, die Gleichung
(2) wird also z.B. die Form:
y = b₁ cos π/2 x/a
+ b₃ cos 3π/2 x/a + b₅ cos 5π/2 x/a + etc.
annehmen, und in dieser den früheren Anforderungen an sie noch
vollkommen entsprechen.
II. Curven von der Tangente
aus.
Für das Abstecken von der Tangente aus würde die Gleichung einer einzigen
Verbindungscurve, welche zu beiden Seiten von C
symmetrisch ist und sowohl in A als in B eine Krümmung Null hat, noch zusammengesetzter als von
der Sehne aus mit dem Anfang in A; für ein Curvenstück
von A bis C dagegen und wenn
nur ein Bestimmungsstück vorausgesetzt wird, kann die
algebraische Gleichung sehr einfach werden; denn es genügen den Anforderungen alle
Gleichungen von der Form:
5) y = b (x/a)n,
wenn darin n > 2 ist. Man hat
nämlich allgemein
dy/dx =
n b/a (x/a)n–
1, d²y/dx² = n(n – 1) b/a² (x/a)n– 2
und die Bedingungen, welchen unsere Curve genügen muß, sind
nun
1) daß in A für x = 0 sowohl
y und dy/dx als d²y/dx² Null wird, was
immer erfüllt wird, wenn n – 2 > 0;
2) daß wenn a und b die
Coordinaten AE und EC des Scheitels C bedeuten (wie denn x = a und y = b zusammengehörige
Werthe der Gleichung (5) sind) man auch zusammen hat x =
a und dy/dx = cot α,
also
n b/a = cot α, a = nb tang
α,
womit die nothwendige Beziehung zwischen den beiden Constanten
a und b der Gleichung
(5) gegeben ist, und diese Gleichung die bestimmtere Form:
y = 1/n a cot
α (x/a)n
annimmt. Man findet dann ferner für unsere Bestimmungsstücke
die Werthe und gegenseitigen Beziehungen:
Textabbildung Bd. 170, S. 13
welche zwar weniger einfach sind als die aus den früheren
Gleichungen abgeleiteten, welche aber zeigen, daß sich aus demselben f mit verschiedenen Werthen von n verschiedene Werthe für die übrigen Bestimmungsstücke t und ρ ergeben, und
daß deßhalb der Exponent n innerhalb gewisser Grenzen
noch eine zweite Constante ersetzen kann.
Die einfachste nicht algebraische Gleichung für den jetzigen Fall dürfte unter
entsprechender homogener Form folgende seyn:
6) y = k (φ – sinφ) = k (π/2 x/a
– sin π/2 x/a);
man zieht daraus
dy/dx = π/2 k/a (1 – cos π/2 x/a), d²y/dx² = π²/4 k/a² sin π/2
x/a
und findet außer der Befriedigung der obigen Bedingung sub 1) im Punkt A für den
Punkt C
x = a, y = b = k (π/2 – 1), cot
α = π/2 k/a, d²y/dx² =
π²/4 k/a².
Damit ergeben sich die Beziehungen:
Textabbildung Bd. 170, S. 13
und als die geeignetste Form der Gleichung (6) für die
Berechnung der y nach der Sexagesimaltheilung
y = x cot
α – 2/π a cot α sin
x/a 90°.
Die Vergleichung der vorhergehenden Werthe der Bestimmungsstücke mit den aus der
algebraischen Gleichung (5) abgeleiteten zeigt übrigens, daß die letzteren den
ersteren durch Bruchwerthe von n so nahe gebracht werden
können als man will, daß daher die Gleichung (5), die auch für die Berechnung
einfacher ist, in der Anwendung immer der Gleichung (6) wird vorzuziehen seyn.
Unter den Verhältnissen unserer Bestimmungsstücke hat meistens das der Tangente t zu dem kleinsten Krümmungshalbmesser ρ das größte Gewicht, weil man sehr oft in den
Fall kommt, zu einer gegebenen Tangente den kleinsten Krümmungshalbmesser zu suchen,
namentlich dann, wenn die Verbindung zweier geraden Strecken durch zwei Curven von
entgegengesetzt gerichteter Krümmung herzustellen ist, und weil es dann viel darauf
ankommt, daß dieser kleinste Krümmungshalbmesser möglichst groß wird. Es ist daher
ein weiterer Vorzug unserer Gleichung (5), daß mit entsprechenden Werthen von n jenes Verhältniß t : ρ nicht nur größer wird, als bei den anderen
Curven (1) bis (4), sondern selbst günstiger als bei dem Kreis. Man hat nämlich bei
der Curve (1), wo das genannte Verhältniß am größten ist,
ρ = 2/3 t sin²α/cos α,
beim Kreis, dessen Halbmesser r
ist
r = t tangα
und bei der Curve (5)
Textabbildung Bd. 170, S. 14
und schließt daraus, daß für kleine Winkel α der letztere Werth immer größer werden kann als
die beiden vorhergehenden, da diese sich dem Werthe Null nähern, jener dagegen dem
Werthe n/(n – 1) t, welcher jedenfalls > t.
Setzt man dann die beiden ρ aus (1) und (5)
einander gleich, so folgt die Bedingung
3n = 2(n
– 1) sin²α + 2 (n – 1)² sin⁴α
und wenn man sin α = 1
setzt, so wird einfach
2n = 5, n
= 5/2
dieser Werth genügt noch den Bedingungen der Gleichung (5) und
spricht aus, daß für n = oder < 5/2, das Verhältniß t : ρ bei (5) für
alle Winkel α größer ist, als bei Gleichung
(1).
Vergleicht man dann die Curve (5) ebenso mit dem Kreis, so ergibt sich die
Bedingung
n = (n
– 1) sin α + (n – 1)² sin³ α
und für sin α = 1 folgt n = 2; man ersieht daraus, daß jenes Verhältniß bei der
Curve (5) dem beim Kreise für die größten Winkel α um so näher kommt, je mehr sich n
seiner Grenze 2 nähert, daß es also für ein α
< 90° immer ein n > 2 gibt, durch welches
das betreffende Verhältniß größer werden kann als bei der
Kreisbogen-Verbindung. Für den kleinsten ganzen Werth n = 3 wird die vorhergehende Bedingung
3 = 2sin α + 4 sin³ α
und gibt sin α = 0,728, α = 46° 43'; es ist demnach jenes
Verhältniß t : ρ für
n = 3 und ein α
< 46 3/4° bei der Curve (5) größer, für ein α > 46 3/4° kleiner als beim Kreisbogen. Für n = 5/2 ist dieser Grenzwerth von α bei 56°, für n = 7/3 bei 60
1/2°, u.s.f.
Schließlich ist noch zu zeigen, daß bei dieser Curve (5), welche dem Vorhergehenden
zufolge in den meisten Fällen den Anforderungen an eine solche Verbindungscurve am
besten genügen wird, die Bestimmungsstücke einfach construirt werden können, und daß
sich damit die Curve selbst ohne Rechnung mit hinreichender Genauigkeit in einen
Situationsplan eintragen läßt. Jene Construction wird am einfachsten, wenn f als gegeben vorausgesetzt wird. Diese Länge f = SC auf die den
Winkel MSN
Fig. 24,
halbirende Gerade SO aufgetragen, bestimmt den
Scheitel C; wird dann durch diesen die Tangente Ca senkrecht zu SO gezogen, so gibt die Senkrechte CE zu
SM durch den Abschnitt aE die Länge b tang
α, und diese von E aus auf EM
n-mal aufgetragen bestimmt nach den
Beziehungen:
a = nb tang α und t = a + f cos α
den Anfangspunkt A der Curve, da
SE = f cos
α ist. Man hat aber auch Sa = f sec α, und wenn aF senkrecht zu Sa gezogen worden, SF = f sec ²α, und daraus ergibt sich der Krümmungshalbmesser
SJ = ρ für
den Scheitel C gleich n/(n – 1) × SF oder FJ = 1/(n – 1) SF. Für n = 3, wie in Fig. 24, hat man also EA = 3 Ea, FJ = 1/2 SF; für
n = 5/2, wird EA =
2 1/2 × Ea, FJ = 2/3 SF, u.s.f. Trägt man nun SJ von C aus nach O auf und beschreibt von O
aus den Krümmungskreis mCn, so läßt sich die Curve
mit hinreichender Sicherheit an diesem fort von C aus
nach den Punkten A und B
hinführen, und es ist selbstverständlich, daß wenn der Krümmungskreis die Tangenten
AS und BS
schneidet wie in Fig. 24, die
Curve auf der concaven Seite, wenn nicht, auf der convexen Seite dieses Kreises
bleiben muß.
Soll ρ das gegebene Bestimmungsstück seyn, so
trägt man diese Länge von S nach J auf die SO auf, nimmt SF = (n –
1)/n
SJ, fällt auf SM die
Senkrechte Fa, und erhält damit die Punkte a, b und C und dann wie
vorher das Uebrige. Ist dagegen t = SA gegeben, so ist es am einfachsten einen
beliebigen Punkt C' anzunehmen, damit den entsprechenden
Punkt A' wie vorher zu bestimmen und nun die SC als vierte Proportionale zu SA, SA' und SC' zu suchen.
Eine Erweiterung der Gleichungen (5) und (6) auf mehrere unabhängige Constanten kann
in ähnlicher Weise, wie es für die Gleichungen (1), (2) und (4) gezeigt wurde,
erhalten werden.
Tafeln