| Titel: | Ueber den Regulir- und Absperrapparat mit indirecter Uebertragung für hydraulische Motoren. Dr. R. Proell's Patent. |
| Fundstelle: | Band 231, Jahrgang 1879, S. 213 |
| Download: | XML |
Ueber den Regulir- und Absperrapparat mit
indirecter Uebertragung für hydraulische Motoren. Dr. R. Proell's Patent.
Mit Abbildungen im Text und auf Tafel 11.
(Schluſs von S. 118 dieses Bandes.)
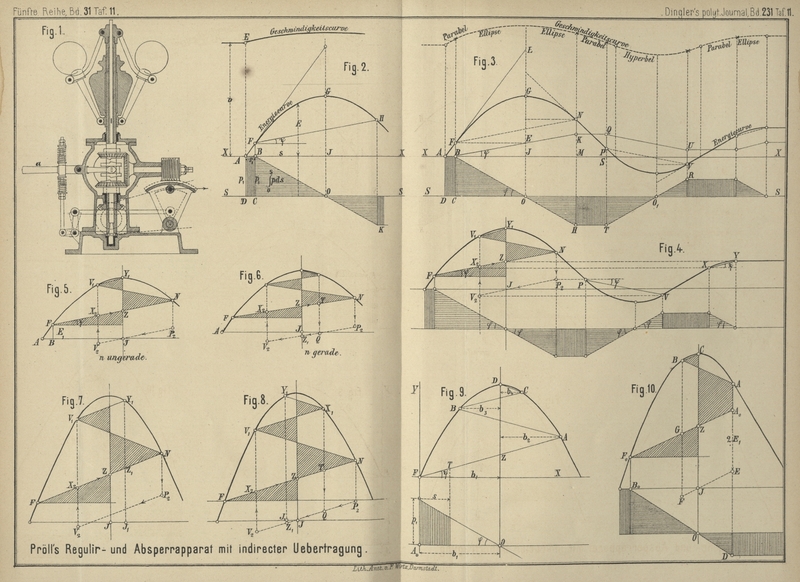
Pröll's Regulir- und Absperrapparat.
Specialfall. Wir haben bisher angenommen, die
Federspannung allein besorge die Auslösung; dies wird jedesmal eintreten, wenn der
Zahnsector im Apparat bei seinen Ausschlägen nicht in die Grenzstellungen geräth.
Wenn indeſsen sehr bedeutende Gleichgewichtsstörungen im Gange des Motors vorkommen,
so kann unter Umständen der Zahnsector durch fortgesetztes Zu- bezieh. Aufschützen
eher in seine äuſserste Stellung gelangen, als die Auslösung im Wendegetriebe
erfolgt ist. Es würde dann nothwendig ein Bruch eintreten. Um dies zu verhindern,
sind die Federn auf der Auslösungsstange am Apparat mit Kapseln versehen, welche
sich in den Grenzstellungen des Schützen fest auf einander legen und die Auslösung
in dem Momente veranlassen, in welchem gerade der Schützen in seine höchste bezieh.
tiefste Lage gelangt. Nachdem dies geschehen, kann dann der Regulator ruhig
fortrotiren, bis er in Folge veränderter Energie aufs Neue kuppelt.
Im Diagramm läſst sich nun dieser Vorgang, wie folgt, darstellen. Wir beginnen die
Construction desselben genau so wie früher (Fig. 10),
zeichnen zunächst die Energieparabel und vom Anfangspunkt F0 derselben die erste Federdruckgerade
und dieser entsprechend die Verstellungsgerade B0OD des Schützen. In
D gelange der Schützen schon in seine tiefste Lage,
d.h. in dem dem Punkte D entsprechenden Punkte A0 der
Federdruckgeraden legen sich gerade die Kapseln auf einander, in Folge dessen die
Auslösung im Wendegetriebe sofort erfolgt; dementsprechend wird also von A0 eine Verticale
aufsteigen, welche in A die Energieparabel schneidet.
Von A aus beginnt dann wieder der bekannte Linienzug
ABC. Statt lauter Dreiecke erscheinen Dreiecke und
ein Trapez. Dieselben sind in Fig. 10
durch Schraffur angedeutet.
Der zur Bestimmung der unausgeglichenen Energie von uns eingeführte Linienzug beginnt
von A0 , geht nach E, welcher Punkt um die Strecke 2 E1 unter A0 liegt, und dann in
bekannter Weise durch FG nach Z, so daſs wir also in der Strecke ZJ wieder
die unausgeglichene Energie erhalten. Die arithmethische Progression der Gröſsen b und p ist unterbrochen,
schreitet aber hinter der Unterbrechung wieder gesetzmäſsig weiter.
Ungleichförmigkeitsgrad. Die Gleichung (30) ist noch
einer weiteren Ausführung fähig. Wir bezeichneten mit Ez den Abstand ZJ bezieh. Z1
J in Fig. 5 und
6. Da beide Fälle im Verlauf der Regulirung gleich oft eintreten können,
so setzen wir:
E_z=ZJ bezieh.
=Z_1J=b_1\,tg\,\psi\pm(E_0+E_2). (32)
Wir erhalten somit nach Gleichung (30):
i_{max}=\frac{b_1\,tg\,\psi+(E_0+E_2)}{A} . .
. . . (33)
und
i_{min}=\frac{b_1\,tg\,\psi-(E_0+E_2)}{A} . .
. . . (33a)
Es ist nun nach Gleichung (17): tg\,\psi=\frac{2\,T_m}{s_m}.
Bezeichnen wir mit k den aliquoten Theil der
Maximalpferdestärken Nm, welcher einbezieh. ausgerückt wurde, so ist derselbe
N=kN_m und analog p=kp_m,
s=b_1=ks_m, folglich ist nach Gleichung (17):
\frac{b_1\,tg\,\psi}{b_1}=\frac{2\,T_m}{s_m} oder
\frac{b_1\,tg\,\psi}{ks_m}=\frac{2\,T_m}{s_m} somit
b_1\,tg\,\psi=2\,kT_m. Setzen wir diesen Werth in die
Gleichung (33) für i ein, so folgt:
i_{max}=\frac{1}{A}[2\,kT_m+(E_0+E_2)] . . . .
(34)
i_{min}=\frac{1}{A}[2\,kT_m-(E_0+E_2)] . . . .
(34a)
oder mit Berücksichtigung der Beziehungen:
\frac1A=\frac{l}{{v_0}^2} und
\frac1l=\frac{2\,Ph}{g}\,\frac{u^2}{U^2}\,\frac{1}{R^2}:
i=\frac{g\,U^2R^2}{2\,Ph\,u^2{v_0}^2}[2\,kT_m\pm(E_0+E_2)].
Berücksichtigen wir, daſs wir mit v0 die anfängliche Peripheriegeschwindigkeit des
Massentheilchens im Kreise vom Radius R bezeichneten,
also v_0=\Omega R setzen können, ferner
\frac{U^2}{u^2}=\frac{\Omega^2}{\omega^2}, so folgt:
i=\frac{g}{2\,Ph\omega^2}[2\,kT_m\pm(E_0+E_2)]
. . . . (35)
Aus dieser Gleichung läſst sich nun erkennen, von welchen Werthen der
Ungleichförmigkeitsgrad i abhängt. Wir sehen, daſs der
gröſste Werth des
Ungleichförmigkeitsgrades i um so kleiner ausfällt, je
kleiner der Werth (2\,kT_m+E_0+E_2), also 1) je kleiner die
Maximalfederspannung, d.h. also je elastischer die Feder ist; 2) je kleiner der
Energieverlust (E_0+E_2), d.h. also je schneller die Umkupplung
im Wendegetriebe erfolgt.
Bei der Frictionskupplung fällt, namentlich wenn der Schützenwiderstand bedeutend
ist, der Werth E2
bedeutend gröſser aus als bei der Zahnkupplung, weswegen letzterer in dieser
Hinsicht der Vorzug zu geben ist. Den Werth k, als Maſs
der Gleichgewichtsstörung, betrachten wir als gegeben, ebenso die Werthe P, h, ω als Constructionsgröſsen für den Apparat.
Diese Vorschriften werden indeſs noch modificirt, wenn wir die gleiche Untersuchung
in Bezug auf die Zeit t anstellen, welche vom Moment
der Gleichgewichtsstörung bis zum Eintritt des neuen Beharrungszustandes
verflieſst.
Ausgleichszeit. Wir nennen den Weg, den das
Massentheilchen m im Diagramm bis zum Eintritt des
neuen Beharrungszustandes zurücklegt, σ und setzen
t=\frac{\sigma}{v_0}. Streng genommen müſsten wir bilden:
t=\int\frac{d\sigma}{dv}, da v0 an jeder Stelle des Weges eine andere
Gröſse hat. Beachten wir aber, daſs die ursprüngliche Geschwindigkeit v0 sich nur wenig
ändern soll, was wir ja gerade durch unseren Regulirapparat bezwecken, so werden wir
obige einfache Beziehung t=\frac{\sigma}{v_0} als zurecht
bestehend anerkennen können.
Zur Bestimmung des Weges a müssen wir die Basen
sämmtlicher Beschleunigungsrechtecke und Dreiecke addiren. Es ist zunächst die Summe
aller Dreiecksbasen:
\sigma_1=(b_1+2\,b_2+2\,b_3+\ldots\,2\,b_n).
Führt man b_2=b_1-a;
b_n=b_1-(n-1)\,a ein, so folgt:
\sigma_1=b_1+2\,(b_1-a)+2\,(b_1-2\,a)+2\,(b_1-3a)+\ldots\,2\,[b_1-(n-1)\,a]
\sigma_1=b_1+2\,(n-1)\,b_1-2\,[a+2\,a+3\,a+\ldots\,(n-1)\,a]=b_1(2\,n-1)-an\,(n-1)=b_1(2\,n-1)-an\,(n-1).
Nun ist a=\frac{b_1}{n}, somit:
\sigma_1=b_1\,(2\,n-1-n+1)=nb_1 . . . .
(36)
Die Summe der Basen der Rechtecke ist:
\sigma_2=\frac{J}{2\,p_1}+\frac{J}{p_2}+\frac{J}{p_3}+\ldots\frac{J}{p_n}.
Wir fanden nach Gleichung (27)
p_n=p_1-(n-1)\,e, somit folgt:
\sigma_2=\frac{J}{2\,p_1}+\frac{J}{p_1-e}+\frac{J}{p_1-2\,e}+\frac{J}{p_1-3\,e}+\ldots\frac{J}{p_1-(n-1)\,e}.
Für n=1 wäre, da
e=\frac{p_1}{n} ist,
\sigma_2=\frac{J}{2\,p_1},
für
n=2:\;\sigma_2=\frac{J}{2\,p_1}+\frac{2\,J}{p_1},
für
n=3:\;\sigma_2=\frac{J}{2\,p_1}+\frac{3\,J}{2\,p_1}+\frac{3\,J}{p_1},
für
n=4:\;\sigma_2=\frac{J}{2\,p_1}+\frac{4\,J}{3\,p_1}+\frac{4\,J}{2\,p_1}+\frac{4\,J}{p_1};
somit ist ersichtlich, daſs für n=n:
\sigma_2=\frac{J}{2\,p_1}+\frac{nJ}{p_1}\left(\frac{1}{n-1}\ldots\frac14+\frac13+\frac12+1\right).
Die Reihe in der Klammer gibt nur endliche Werthe für endliche
Werthe von n. Setzen wir:
1+\frac12+\frac13+\frac14+\ldots\frac{1}{n-1}=S, so folgt
\sigma_2=\frac{J}{p_1}\left(\frac12+nS\right),
Somit folgt nun, da
\sigma=\sigma_1+\sigma_2 ist:
\sigma=nb_1+\frac{J}{p_1}\left(\frac12+nS\right), . . . . .
. . . . . . . (37)
daher
t=\frac{\sigma}{v_0}=\frac{nb_1+\frac{J}{p_1}\left(\frac12+nS\right)}{v_0}
. . . . . . . . . . . . (38)
Es ist nach Gleichung (9) J=2\,l\,(E_0+E_2); dies in Gleichung
(38) eingeführt, ebenso l=\frac{g}{2\,Ph}\,\frac{\Omega^2R^2}{\omega^2}, und da
v_0=\Omega R gesetzt werden kann,
\frac{l}{v_0}=\frac{g}{2\,Ph}\,\frac{\Omega R}{\omega^2} so
folgt:
t=\frac{nb_1}{\Omega
R}+\frac{E_0+E_2}{p_1}\,\frac{g}{Ph}\,\frac{\Omega
R}{\omega^2}\left(\frac12+nS\right) . . . . (39)
Nach Gleichung (28a) ist n umgekehrt proportional zu tg ψ. Würden wir aus dem Apparat die auslösenden Federn
fortnehmen, so würde sich der Apparat in Nichts von einem gewöhnlichen
Regulirapparat mit indirecter Uebertragung unterscheiden.
Wenden wir auf diesen Fall unsere Gleichungen an, so würde in Gleichung (17)
T_m=0 zu setzen sein. Wir würden dann
tg\,\psi=0 erhalten und nach Gleichung (28a)
n=\infty. Führen wir diesen Werth in Gleichung (39) ein, so
sehen wir, daſs auch t=\infty wird, d.h. ein Ausgleich tritt
theoretisch erst nach unendlich langer Zeit, also nie ein. Dies Resultat steht in
Uebereinstimmung mit dem Urtheil, welches wir oben über die Anwendung des
Wendegetriebes als alleinigen Mechanismus bei der indirecten Regulirung fällten.
In der Gleichung (39) können wir nun für eine bestimmte Gleichgewichtsstörung bei
einer vorhandenen Anlage die Werthe ΩR als constant
ansehen. Es folgt dann, daſs t um so kleiner ausfällt,
also der neue Beharrungszustand um so schneller eingeleitet wird, 1) je kleiner der Energieverlust
E_0+E_2, d.h. je empfindlicher und energischer der Regulator
im Wendegetriebe die entgegengesetzte Drehrichtung einleitet; 2) je gröſser p1 d.h. da p1 umgekehrt
proportional zur trägen Masse M des Motors ist, je
kleiner M ist und 3) je kleiner der Werth n ist, denn damit verringert sich auch der Klammerwerth
S. Das Diagramm läſst sofort erkennen, daſs n um so kleiner ausfällt, d.h., daſs die Anzahl der
Geschwindigkeitswellen um so geringer, je gröſser der Winkel ψ ist.
Da nun nach Gleichung (17) tg\,\psi=\frac{2\,T_m}{s_m} ist und für
den als gegeben anzunehmenden Werth s_m\,tg\,\psi mit Tm wächst, so muſs Tm möglichst groſs
gewählt werden. Diese Bedingung steht aber im geraden Widerspruch zu der Bedingung 1
bei der Bestimmung von i.
Mit der Verstärkung der Feder verringert sich die Ausgleichszeit, vergröſsert sich
aber der Ungleichförmigkeitsgrad. Da es nun aber in der Praxis wünschenswerth ist,
nicht allein den Ungleichförmigkeitsgrad, sondern auch die Ausgleichszeit möglichst
klein zu erhalten und wir beiden Bedingungen gleichzeitig nicht gerecht werden
können, so wird eine nach der Gröſse des Apparates und nach der trägen Masse M und der Geschwindigkeit ΩR des Motors sich richtende und auf die Kupplungshülse reducirte
Federspannung Tm = 2
bis 3k zu wählen sein; die Bestimmung der
Federspannung Tm ist
mehr Sache des praktischen Versuches. Um Federn von verschiedener Stärke leicht
einsetzen zu können, kann die Anslösungsstange mit den Kapseln sehr leicht demontirt
werden.
Es soll nun zunächst nach den hergeleiteten Beziehungen ein Beispiel berechnet
werden.
Beispiel. Der
Regulirapparat bewege den Regulirschützen einer Zeidler'schen Turbine (*1877 224 134). Das
Laufrad derselben habe einen Radius R=1^m,500; die Turbine
übertrage bei voller Schützenöffnung auf die Hauptwelle N_m=90^e.
Die Tourenzahl der Turbine in der Minute sei U=24. Dann ist nach
Gleichung (11) die Umfangskraft im Laufradkreis von
R=1^m,500:
K_m=\frac{716,2\,N_m}{UR}=\frac{716,2\times
90}{24\times 1,5}=1790^k.
Sämmtliche auf den Kreis vom Radius R
reducirt gedachte und in Rotation befindliche Masse sei auf
M=1000 veranschlagt (bezogen auf Meter als Einheit für die in
M steckende Beschleunigung der Schwere). Dann folgt
die dem Werthe Km
entsprechende beschleunigende Kraft für die Masseneinheit:
p_m=\frac{K_m}{M}=\frac{1790}{1000}=1^k,790.
Wir nehmen nun an, die Turbine arbeite mit halber Maximalkraft,
also N=45^e, und dementsprechend befinde sich sowohl der
Zahnsector am Apparat, als auch der Schützen in seiner mittleren Stellung. Bewegende
Kraft und Widerstand halten sich genau das Gleichgewicht. Es möge nun die Hälfte, d.
s. 22e,5, ausgerückt werden, so daſs unser früher
eingeführter Begriff k den Werth = ¼ annimmt. Zu
beantworten sind nun die Fragen: 1) Wie groſs ist der nach
der Ausgleichung zurückbleibende Ungleichförmigkeitsgrad im Gange der
Turbine? 2) In welcher Zeit wird der neue
Beharrungszustand erreicht?
Die totale Verstellungszeit des Schützen betrage tm = 6,5 Secunden, d.h.
in dieser Zeit werde bei normaler Geschwindigkeit der Turbine der Schützen aus
seiner tiefsten Lage in seine höchste gehoben. Nach Gleichung (15) ist nun:
s_m=\frac{R\,\pi\,U}{30}\,t_m=1,5\times
2,51\times 6,5=24^m,47.
Es sei die auf die Kupplungshülse reducirte Maximalfederspannung
T_m=3^k gewählt. Dann folgt nach Gleichung (17):
tg\,\psi=\frac{2\times
3}{24,47}=0,245,
welchem Werthe ein Winkel
\psi=13^{\circ}40' entspricht.
Zur Bestimmung der Constanten l nach
Gleichung (4) nehmen wir an, daſs für den Regulator P=15^k die
durch den Mechanismus gegebene Strecke h=0^m,23 und die
Tourenzahl u der Regulatorspindel = 80 ist. Es folgt
dann:
\frac1l=\frac{2\times 15\times
0,23}{9,81}\,\frac{80^2}{24^2\times 1,5^2}=3,43, somit
l=0,291.
Wir setzten weiter:
\frac1A=\frac{l}{{v_0}^2}=\frac{l}{\Omega^2R^2}=\frac{0,291}{2,51^2\times
1,5^2}=\frac{1}{49,1}.
Behufs Feststellung des Energieverlustes
E_1=E_0+E_2 nehmen wir an, der Regulirapparat sei mit einer
Zahnkupplung im Wendegetriebe versehen. Die Kupplungshülse sowohl, als das obere und
untere Rad habe nur je einen Mitnehmerzahn, welcher eine solche Abschrägung besitzt,
daſs bei einer Berührung der Zahnflächen und einem dem Bewegungswiderstande des
Schützen entsprechenden Zahndruck durch die Abschrägung hervorgerufene
Kraftcomponente die in der Richtung der Zahnfläche in Folge des übertragenen
Zahndruckes entstehende Reibung tödtet. (Siehe die weiter unten folgende
Berechnung.) Bei dieser Einrichtung resultirt sowohl für E0 als für E2 ein sehr kleiner Werth. Wir setzen
denselben E_1=E_0+E_2=0,5+1=1^k,5, somit folgt nach Gleichung
(34):
i=\frac1A\,(2\,kT_m\pm
E_0+E_2)=\frac{1}{49,1}\left(\frac{2\times
3}{4}\pm1,5\right)=rot\;0,061\;\text{bezieh.}\;0.
Wenn also die Turbine vor der Gleichgewichtsstörung mit 24 Touren
in der Minute lief, so läuft sie im ungünstigsten Falle nach erfolgtem Ausgleich mit
der constanten Tourenzahl von 24\times 1,061=25,46, im
günstigsten Falle aber mit derselben Tourenzahl 24 weiter.
Wird obige Abweichung für zu hoch befunden, so gibt Gleichung (35)
die Mittel an, wie der Werth von imax zu verkleinern ist. Es würde dies z.B. durch Vergröſserung
von ω, also durch eine höhere Tourenzahl des Regulators
zu erreichen sein. Andererseits muſs aber auch beachtet werden, daſs ebenso oft auch
der Ausgleich der Geschwindigkeitswelle so vor sich gehen kann, daſs das Glied
E_0+E_2 subtractiv wie in Gleichung (34a) angenommen
erscheint, in welchem Falle dann i=0 ist.
Der Maximalwerth von i tritt ein,
wenn die Anzahl n der Dreiecksflächen in Fig.
5 ungerade, der Minimalwerth von i dagegen,
wenn der Werth n gerade ist. Da nun zu erwarten steht,
daſs n in Wirklichkeit weder einen ungeraden, noch
geraden Werth annehmen wird, so wird auch der wahre Ungleichförmigkeitsgrad zwischen
den Werthen 0 und 0,061 liegen und zwar in dem Maſse näher an 0 bezieh. 0,061, als
der aus Gleichung (28a) bestimmte Werth n sich mehr
einer geraden bezieh. ungeraden Zahl nähert.
Zur Berechnung von n benutzen wir
Gleichung (28a). Da nun p_1=kp_m=\frac{1,790}{4}=0,4475 ist, so
folgt n=\frac{0,4475}{2\times 0,291\times 0,245}=3,14.
Die Ausgleichszeit ist nach Gleichung (38) zu bestimmen, in
welcher:
b_1=ks_m=\frac{24,47}{4}=6,12
J=(E_0+E_2)\,2\,l=1,5\times 2\times
0,291=0,873;
ferner ist, für den angenäherten Werth
n=3,
S=1+1/2=1,5, endlich v_0=\Omega R=2,513\times
1,5=3,77. Somit folgt:
t=\frac{3,14\times 6\times
12+\frac{0,873}{0,4475}\,(0,5+3,14\times
1,5)}{3,77}=7,8\;\text{Secunden}.
Also in 7,8 Secunden ist der
neue Beharrungszustand erreicht.
Vorstehende Rechnung zeigt, wie leicht und verhältniſsmäſsig
schnell nach den aufgestellten Gleichungen in jedem einzelnen Falle der Verlauf der
Regulirung rechnerisch verfolgt werden kann.
Schluſsbemerkung. Im vorstehenden
Beispiel führten wir bereits an, wie man durch richtige Abschrägung des
Mitnehmerzahnes in der Kupplung in der Lage sei, den Werth E0 möglichst klein zu machen. Es soll noch
im Folgenden der Winkel der Abschrägung bestimmt werden.
Textabbildung Bd. 237, S. 219In nachstehender Figur bedeute α den Winkel,
welchen die Zahnfläche mit der Verticalen bilden muſs, damit die zum Ausrücken der
Kupplung vom Regulator zu leistende Arbeit ein Minimum werde. Der durch den
Kupplungszahn übertragene horizontale Druck T zerlegt
sich normal und parallel zur Zahnfläche. Die normale Componente ist
N=T\,cos\,\alpha, also beträgt die der Ausrückung der
Kupplungshülse entgegenwirkende Reibungskraft
N\mu=T\mu\,cos\,\alpha. Auſser dieser wirkt an der verticalen
Fläche des Keiles, durch welchen sich die Torsionskraft der Regulatorspindel auf die
Kupplungshülse überträgt, die Reibung R.
Bezeichnet man wie früher mit E die Energie des
Regulators, so muſs angenähert sein:
T\,sin\,\alpha+E=T\mu\;cos\,\alpha+R.
Eine genauere Gleichung erhält man, wenn man T sin α und
Tμ cos α noch einmal in die Richtung von E zerlegen würde. Man würde dann die Beziehung
erhalten:
T\,sin\,\alpha\,cos\,\alpha+E=T\mu\,cos\,\alpha\,cos\,\alpha+R.
Die letztere Gleichung führt auf eine Gleichung höheren Grades zur Bestimmung von
a. Da aber Winkel a
ziemlich klein ist, so erscheint die zuerst aufgestellte Gleichung genau genug.
Wenn der Regulator keine Arbeit beim Ausrücken der Kupplung leisten soll, so muſs in
obige Gleichung E=0 eingeführt werden; d.h. es muſs die Bedingung
T\,sin\,\alpha=T\mu\,cos\,\alpha+R erfüllt sein.
Ist μ1 der
Reibungscoëfficient am Keil, r der Abstand der
Spindelmitte von Mitte Keil und ρ derselbe von Mitte
Zahnfläche, so folgt:
T\,sin\,\alpha=T\mu\;cos\,\alpha+T\mu_1\,\frac{r}{\varrho}
oder sin\,\alpha=\mu\,cos\,\alpha+\mu_1\,\frac{r}{\varrho}, d.h.
es ist, wie zu erwarten stand, der Winkel α unabhängig
von der durch die Kupplung übertragenen Tangentialkraft T, also auch unabhängig von dem Widerstand,
welchen der Schützen zu seiner Bewegung erfordert. Es ist dies ein sehr wichtiges
Resultat, da hierdurch der Werth E0 zu einer Constanten des Apparates wird.
Zur numerischen Berechnung von a
führen wir die Werthe \mu=0,10 als Reibungscoëfficient von Stahl
auf Stahl bei guter Schmiere und \mu_1=0,13 als
Reibungscoëfficient am Keil ein, wegen leichter Verdickung der Schmiere etwas
groſser angenommen. Ferner setzen wir \frac{r}{\varrho}=1,5,
somit folgt:
sin\,\alpha=0,1\,cos\,\alpha+0,13\times
1,5 oder
1-cos^2\alpha=(0,1\,cos\,\alpha+0,2)^2.
cos\,\alpha=\pm\;0,975-0,01985.
Nur der eine Werth
cos\,\alpha=+\;0,95515 ist hier brauchbar. Wir erhalten
\alpha=17^{\circ}10'.
Es ist also zweckmäſsig bei der Ausführung der Kupplung, wenn obige Voraussetzungen
erfüllt sind, dem Zahn möglichst die Abschrägung
\alpha=17^{\circ}10' zu geben.
Schlieſslich bedarf noch eine besondere Einrichtung am Apparat der Erwähnung, nämlich
diejenige, mit welcher es möglich ist, mit dem Apparat die beaufschlagenden
Wassermassen ganz abzusperren, d. i. also nach Willkür den Schützen vollständig zu
senken. Zu dem Ende ist nur nöthig, die als Handgriff ausgebildete Verlängerung des
Auslösungshebels abwärts zu drücken und dadurch den Regulator in seine höchste Lage
zu heben. Auf diese Weise wird künstlich ein Zuschützen eingeleitet, welches so
lange währt, bis der Schützen in seine tiefste Lage gelangt ist und die Kapseln an
der Auslösungsstange eine selbstthätige Senkung des Regulators und damit Auskupplung
veranlaſst haben.
Das Anlassen des Motors erfolgt nun umgekehrt in ebenso leichter Weise, indem man die
Schneckenwelle mittels eines aufgesetzten Schlüssels fortgesetzt so dreht, daſs sich
der Schützen allmälig hebt Dadurch gelangt Wasser auf den Motor, derselbe beginnt
sich zu drehen. Auch die Drehung des Apparates beginnt und die automatische
Regulirung geht vor sich, indem nunmehr der sich selbst überlassene Regulator mit
der Kupplung im Apparat zu spielen beginnt und jede Gleichgewichtsstörung im Gange
des Motors auf die oben beschriebene Weise in verhältniſsmäſsig kurzer Zeit
ausgleicht.
Auf dem Eisenwerk Lauchhammer befindet sich ein Apparat
in Thätigkeit. Er regulirt ein oberschlächtiges Wasserrad sehr gleichmäſsig und
ruhig, wobei er genau das Gesetz der Auslösung zeigt, welches in so übersichtlicher
Weise das oben hergeleitete Diagramm darstellt.
Tafeln